Convolution Neural Networks for Image Categorization

Why

I''m writing this to help developers without a degree in artificial intelligence understand the subject, as most material on the matter is rather complex.  I am also hoping to shore up my own understanding as I am relatively new to the subject of deep learning neural networks. 

What

The problem domain is essentially a function whereby and image is passed in, and one or more categories result, each with an associated probability.

A convolution neural network used for image categorization.

There are many other similar use cases as well, such as gesture recognition but for this article we'll limit discussion to this case.

More technically, a Convolution Neural Network (CNN) is a specific type of deep learning neural network which is comprised of:

• An input layer containing a bitmap.
• Some number of convolution layers, which apply convolution filters and output the result to the next layer.
• Some number of sub-sampling layers, which each downsize the data from the previous layer.
• A fully connected hidden, and a fully connected categorization (output) layer.  Don't worry if you don't know what these things are, we'll cover it.

There are infinite different ways to compose such layers, and this fact has led to CNN design sitting somewhere between an art form and a science.  Each year there are competitions between researchers in attempts to reach new benchmarks in performance and scale.  A well known such competition is hosted by ImageNet, where recent competitions have for instance involved recognizing objects in one of hundreds of categories and even identifying placement of those objects within the image.  From the years of research, there have arisen some recognized "standard" designs which have traditionally given good results for certain domains.

Who

There are several open source frameworks that have arisen for this domain.  A few of them are:

Caffe	Written in C++, is well established, fast, and supports GPU optimization. Originally targeted Linuxy OSes, but has been ported to Windows (in beta as of this writing).
Torch	Written in Lua, also well established and optimized. Currently for Linux and community seems a bit opinionated about remaining there, but there are porting efforts that look to have been somewhat successful. I wouldn't tread here unless you either know and love Lua already, or are prepared to get your feet wet in the same.
Intel Deep Learning Framework	Vectorized CPU and OpenCL GPU implementations in C++ of CNNs and others. Looks like Intel is no longer actively developing on this, but it appears to be pretty mature and might at least inspire optimizations.
CNN Workbench	In C#. There used to be a really nice article on this with a great looking GUI on CodeProject, but the author pulled it down. This link is all I have, which is a fork of just the library part of it. No community to speak of here.
CNNCSharp	In C#. Again no community, but this repo seems to have all the needed goodies.
ConvNetJS	Javascript implementation of CNNs which is easy to try in your browser. Great visualizations.

How

Now we'll take the details step by step.  I'm going to use visualizations from the default network for CIFAR-10 in ConvNetJS to illustrate the process.  The network is structured as follows:

Default network layout for CIFAR-10 in ConvNetJS

Input layer

The first thing that's typically done is to turn the image into a 3D tenser of floating point values; two dimensions for the X and Y pixels and a dimension for the three color channels.  As a reminder, a tenser is simply an n-dimensional array; vectors are 1-dimensional tensors, matrices are 2-dimensional tensors.  The conversion is in order to accommodate the fuzzy math that is coming; such math routines are written to take generic structures of floating point values, not discrete integers such as are used to store bitmap data.

Convolve

First convolution layer.  Uses 16, 5x5 filters (labeled Weights) against the input

A convolution function essentially returns how well a portion of data matches a given filter.  Most filters are some type of edge detector of some angle and perhaps some color combination.  A convolution layer steps in increments of some stride (one in the example) across and down the input data, and outputs how well each position matches the filter.  In the case of the example, the configuration is to use 16 filters for the first convolution layer, so this scanning and outputting is done for each of 16 filters.  You'll notice there are 16 filters (labeled Weights) represented in the image, but the filter size is 5x5x3.  This is because the above visualization combines the 3 color channels into composite (RGB) images.

What you're seeing in the Activations images in the example are pixels representations of how well that part of the image matched the filter, so lighter portions match better.

ReLU

Activation function of first convolution layer brings out only the highlights.

Every intermediate layer of the network has something called an activation function.  The name comes from a biological neuron which only fires (activates) if incoming signals from upstream neurons cumulatively reach some level of signal.  This function's job is to amplify contrast and must be non-linear. The extreme case is a threshold function which turns fully on (1) when the inputs reach a certain level, otherwise is fully off (0).  In practice, most neural networks use hyperbolic tangent, sigmoid, or ReLU functions, which are non-linear, but not fully discreet so as to preserve some uncertainty.  The reason a linear function would not work well is that the entire network would degenerate to grays rather than portions of the network taking on specific features.  The activation function can either be thought of as part of the neural network layer, or a layer of its own.

Pooling

First pooling layer down-samples the result.

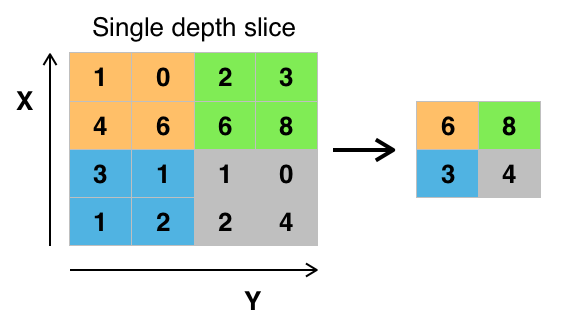Pooling is simply the process of downsizing.  There are different techniques for doing this, the most common for CNNs being using the Max function within a sample segment.  

The reason for pooling is to create a degree of scale invariance and to allow the next layers to match on higher level visual patterns.  The nature of max pooling also creates a degree of rotation invariance because the "max" feature can move a little within each sample segment.

Rinse and Repeat

After this, the Convolution, ReLU, and Pooling processes are repeated, though with variations such as number of convolution filters.  Some networks add back-to-back convolutions without pooling near the end and some nest entire CNNs within each other; clearly there are infinite possibilities.  How is one to know what is best?  The short answer is that this is a design domain, so there will be various trade-offs for each, and the best designs may yet to be discovered.  That said, it is important to know the principles.

The desire is for the network to learn the essential characteristics that constitute the essence of the category.  In order to do this, sufficient layers are needed in order to represent the complexity of the concept.  For example, it is relatively simple to distinguish hand-written characters from each other, compared to recognizing the difference between Corgie and Dachshund dogs in nearly any pose.  To distinguish the latter, sufficient convolution layers must build up from simpler ones.  The first convolution layer basically establishes fundamental edge shapes.  The second recognizes compound shapes such as circles or ripples.  By the time you arrive at the 5th or higher convolution layers, the features are very high level, such as "eyes", "words", etc.  Note that those labels are not necessarily known to the network, but the network will recognize the patterns regardless.  For instance, the actual category of Corgy might fire when the right combination of lower level features are present, such as "eyes", "stubby tail", "short legs".  Yes this is amazing.

So why not just add hundreds of layers with hundreds of filters each?  Performance is one reason, diminishing returns is another.  Though CNNs are quite effecient considering the prospect of trying to accomplish the same feats with fully connected per-pixel deep networks, they are still expensive computationally and memory wise; especially when training.  One promising avenue of research is building networks for new purposes out of networks that were trained for others.  This works, because many of the primitives (such as "eyes") are common in higher level patterns and can be reused.

Fully Connected

The fully connected (FC) layer is essentially a traditional neural network, where every "neuron" coming from the previous layer is "wired" to every neuron in the fully connected layer.  These neuron's decide what combination of features from the convolution layers ultimately constitute each category.  In other words, the FC layer has a neuron for every category, and the connections coming from each neuron (convolution feature) of the previous layer are weighted such that when the correct combination(s) are present, the category scores highly.

Softmax

The fully connected layer determines the categorical probabilities as arbitrary real values.  The final step is to normalize those into probabilities.  Normalization means that rather than just producing a set of arbitrary numbers for each category, the category values are factored together so that the sum of all categories is 1, or at least nearly so.  For this task, the Softmax function is often used because it gives increased weight to the most positive values.

Now What?

Here are some resources to get you going:

• I'd recommend spending a little time with ConvNetJS.
• This article shows how to construct a CNN for the CIFAR-10 dataset.  It is for Torch, but is useful as a detailed expose of CNN construction regardless.  The CIFAR datasets are a good place to start as they are only 32x32 pixels and a relatively simple network works well.
• nVidia DIGITS is software which makes it easy to construct a CNN and run it against nVidia GPUs.
• If you're interested in Torch, there are ready-made Amazon G2 (GPU accelerated) instances such as this one.
• When you're ready for more advanced nets, check out GoogLeNet, AlexNet and others on the Caffe Model Zoo.
• To better understand what these networks are learning and thus improve them, there are efforts to visualize their learning through deconvolution.